Contents |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Subroutines are self-contained parts of a program that, when called, create a new section on the stack and store their local variables there. After terminating, subroutines return to the point exactly where they were called. They also store this return point on the stack.
Furthermore, subroutines can receive arguments that can be different with each call. They can also return a value. These are then called functions. When subroutines or functions appear in conjunction with classes (more on this later), they are called methods of the class.
A typical subroutine that does not return a value is, for example,
void print (double x)
{
System.out.println("Value = " + x);
}
In this context, `void` means that no value is returned. The name of the subroutine in the example is `print` . The subroutine receives an argument called `x` , which must be a double value. An example of the call is:
double x = Math.PI; print(x); // prints: value = 3.14152
The general declaration of a subroutine is therefore
result type name ( parameter list ) instruction block
This is
result type |
Type of return value, or void if no value is returned. |
name |
Name of the subprogram. |
parameter list |
Comma-separated parameters. Each parameter looks like a variable declaration and behaves locally like a variable. The values for these variables are passed when the program is called. |
instruction block |
A sequence of instructions enclosed in {...} , each instruction terminated with ; . |
The terms parameter and argument are usually kept separate. Arguments are the values passed to the parameters.
Note: For reasons that will only become clear later, subroutines
called from main must be declared static .
A complete program looks like this.
public class Test
{ public static void main (String args[])
{
double x=Math.PI;
print(x);
print(x*x);
print(4.5);
}
static void print (double x)
{
System.out.println("Value = "+x);
}
}
So, the static modifier is added.
The `print` function must therefore be declared within the `Test` class. From there, it can be called simply by name from ` main` . We will later learn about subroutines in other classes. These are then called, for example, with `ClassName.print(x)` . In fact, we have already used such calls, for instance, with `Math.sqrt()` .
Important: Note that the `x` in `print` has nothing to do with the `x` in the main program ` main`
.
It is a local variable.
Functions are subroutines that do not have the result type void . They return a value and can therefore be used in expressions. A simple example is the function x^2 .
double sqr (double t)
{
return t*t;
}
The result is returned using the `return` statement . This function can then be used like any other expression. The following example prints the value of this expression.
double x = 1.2;
System.out.println(sqr(x));
System.out.println(sqr(Math.sin(x)) + sqr(Math.cos(x))); // should return approximately 1
Note that in the third line of the example, Math.sin(x) is only calculated once. If you use instead
System.out.println(Math.sin(x)*Math.sin(x));
This means the sine function is calculated twice. However, one could also...
y = Math.sin(x); System.out.println(y*y);
use. This would then mimic the way the function call works, which also uses a local variable (named t ).
Note: The return statement terminates the function from any point - including from within loops.
One advantage of functions is that they hide the underlying technology. You can change the function without having to change the rest of the program. Here's an example.
public class Test
{
public static void main (String args[])
{
String First name="Hans", Last name="Schmidt";
System.out.println(makeName(FirstName,LastName));
}
public static String makeName
(String first name, String last name)
{
return firstname + " " + lastname;
}
}
The function `makeName()` creates a name from the first and last names. If you want the name in a different format, you only need to modify the subroutine, and the function of the program will change wherever it is used. In the example above, this only happens once, but generally, you should consider using subroutines whenever a piece of program code is used more than once.
In this example, the following change would be useful.
public static String makeName
(String first name, String last name)
{
return lastname + ", " + firstname;
}
All variables declared within a function (or a subroutine, which we will no longer distinguish between) are local and no longer exist after the subroutine finishes. They are placed on the stack, and this stack is released after the subroutine completes.
As an example, we will program a function that calculates x^4.
double pow4 (double x)
{
double y=x*x;
return y*y;
}
The variable y is local. Likewise, the parameter x behaves locally like a variable.
Note again that the name and location of a local variable have nothing to do with the calling program, just as little as the name and location of parameters that simply behave like local variables of the subroutine.
Parameters are therefore local. Their memory location is unrelated to the calling program. Parameters are essentially just local variables to which certain values (arguments) are assigned when the program is called. Changing the parameters does not affect the calling program. Their name is irrelevant to the calling program.
public class Test
{
public static void main (String args[])
{
int x=4;
test(x);
System.out.println(x);
}
public static void test (int x)
{
System.out.println(x);
x=5;
}
}
This example prints the number 4 twice, once in the subroutine and then again in the main program. Setting x to 5 in `test` has no effect on `main` . The `x` in `main` is unrelated to the parameter `x` in `test` . Only the value 4 is passed to the subroutine, and this value is assigned to the parameter `x` . In fact, the assignment `x=5` is meaningless.
Parameters are therefore always passed as a value .
In C, there's a simple way to pass parameters as variables or pointers to variables. In this case, the variable changes when the parameter is modified within the subroutine. This can only be replicated in Java using objects. However, passing variables, in particular, is confusing and error-prone, as is passing them as pointers in C.
If a subroutine calls itself directly or indirectly, this is called a recursive call . Since all variables and parameters of the subroutine are local, they do not interfere with the variables and parameters of the previous call.
Such recursions can be used to create very elegant programs. However, each call costs time and stack space. Stack space is also limited, so you have to be careful not to exceed it. Otherwise, you'll get an exception that you'll have to handle.
For example, we calculate the factorial n!=1*2*...*n recursively and elegantly as follows.
double fake (int n)
// Faculty recursively
{
if (n<=1) return 1.0;
else return n*fak(n-1);
}
It is clear that an iterative solution is also an option here, which is faster and only requires stack space for one call.
double fake (int n)
// Faculty iterative
{
double x=1.0;
int i;
for (i=2; i<=n; i++)
{
x=x*i;
}
return x;
}
This solution doesn't look very elegant, however. But elegance can also be a crucial foundation for clarity , maintainability, and therefore, error-free operation . Some programs can only be solved using recursion. When recursion reaches its limits due to limited stack space, one might then mimic recursion using data on arrays. It's clear that recursive functions accomplish this task much more elegantly and transparently.
It is often unclear how the recursive solution actually works. In this case, the individual values of n are temporarily stored on the stack, starting from n and working backwards to 1. When the stack is cleaned up, these values are then used to calculate the multiplication 1*2*3*...*n .
In Java (as in C++, but not in C), functions are distinguished by their parameter types (the so-called signature). The compiler selects the correct function (or subroutine) that can process these parameters.
However, functions are not differentiated according to their result type.
public class Test
{
public static void main (String args[])
{
print(3.4); // prints: double value 3.4
print(3); // prints: int value 3
}
static void print (double x)
{
System.out.println("double value "+x);
}
static void print (int n)
{
System.out.println("int value "+n);
}
}
The two subroutines have the same name. The compiler (or interpreter) distinguishes the functions based on the type of their parameter values. (Functions that differ only in their result type generate an error message.)
Of course, a function can also return an array. It looks like this.
static double[] generate (int n)
// Return an array containing n random variables.
{
double R[]=new double[n];
int i;
for (i=0; i<n; i++) R[i]=Math.random();
return R;
}
The result type is therefore written like an array declaration without a name. The program, of course, only returns a reference to the array. The array itself resides on the heap. Remember that elements on the heap are automatically disposed of when they are no longer needed.
You can also pass an array (more precisely, a reference to it) as a parameter to a function. As an example, we'll write subroutines that calculate the mean and standard deviation. Here's a complete program.
public class Test
{
public static void main(String args[])
{
double R[] = generate(1000);
double m = mean(R);
System.out.println("Mean value " + m);
System.out.println("Standard Deviation " + deviation(R, m));
}
static double[] generate(int n)
// generate a random vector of length n
{
double R[] = new double[n];
int i;
for (i = 0; i < n; i++)
R[i] = Math.random();
return R;
}
static double mean(double x[])
// Calculate the average of x
{
int n = x.length, i;
double sum = 0;
for (i = 0; i < n; i++)
sum += x[i];
return sum / n;
}
static double deviation(double x[], double mean)
// Calculate the standard deviation of x when the mean is
// is known
{
int n = x.length, i;
double sum = 0;
for (i = 0; i < n; i++)
sum += sqr(x[i] - mean);
return Math.sqrt(sum / (n - 1));
}
static double sqr(double x)
// Auxiliary function, calculate x^2
{
return x * x;
}
}
Note that only a single array exists. Everything that is passed or returned is only a reference to this array.
So far, we have only used local variables in subroutines and functions. This is in line with good functional programming practice . However, there are also global variables that can be accessed from any subroutine. Since we have only defined static functions of the class so far, these global variables must also be static.
In the following example, we have defined a global and static counter ` count` . This counter is intended to count how many times the function `f(x)` has been called, the zero of which, between 1 and 2, we want to find using the secant method.
public class Test
{
// Counter for the number of function calls public static int count = 0; public static double f(double x) { count++; return x * x * x - x - 1.0; } public static void main(String args[]) { // Calculate the zero of f using the secant method double xa = 1.0, xb = 2.0, ya = f(xa), yb = f(xb); while (Math.abs(yb) > 1.0e-10) { double xnew = (xa * yb - xb * ya) / (yb - ya); xa = xb; xb = xnew; ya = yb; yb = f(xb); } System.out.println("Result: " + xb); System.out.println("After " + count + " function calls"); } }
The result looks like this:
Result: 1.324717957244746 After 10 function calls
It shows that only 10 function calls are sufficient for 14-digit accuracy. The secant method is a very good method for finding roots.
Java includes automatic documentation generation for functions and classes. When used, this documentation is available in development environments. Hovering the mouse over a function name, for example, displays the documentation.
The necessary comments begin with /** and end with */ . They can contain @ parameters. Eclipse automatically creates an empty comment if /** is entered with a return key. Note that there are simple comment blocks that begin with /* and end with */ .
/** * Test class for demonstrating the secant method. * @author reneg */ public class Test { /** * Counter. */ public static int count = 0; /** * Function whose zero is to be determined. * @param x * @return f(x) */ public static double f(double x) { count++; return x * x * x - x - 1.0; } /** * Calculate the zero of f using the secant method. * @param args (not used) */ public static void main(String args[]) { double xa = 1.0, xb = 2.0, ya = f(xa), yb = f(xb); while (Math.abs(yb-ya) > 1.0e-20) { double xnew = (xa * yb - xb * ya) / (yb - ya); xa = xb; xb = xnew; ya = yb; yb = f(xb); } System.out.println("Result: " + xb); System.out.println("Function value : " + f(xb)); System.out.println("After " + count + " function calls"); } }
It is rather unusual to also add JavaDoc comments to variables . Usually, only // comments are used here.
Here again is the bisection method with functions. The program then looks much clearer.
public class Test
{
public static void main (String args[])
{
System.out.println(bisect(0,1));
}
static double bisect (double a, double b)
// Bisection method for the function x
{
double m,y;
while (ba>1e-13) // Terminate if interval is small enough
{
m=(a+b)/2; // Calculate the middle
y=f(m); // and value in the middle
if (y>0) a=m; // Take right half-interval
else b=m; // Take left half-interval
}
return (a+b)/2;
}
static double f (double x)
// Function whose zero is calculated
{
return Math.exp(x)-4*x;
}
}
The disadvantage is that the function f , whose zero is to be calculated, cannot be so easily passed to the function bisect (unlike in C). However, there are various workarounds.
There are problems that can almost only be solved using recursion. One of them is the Towers of Hanoi problem.
The initial situation is outlined here.
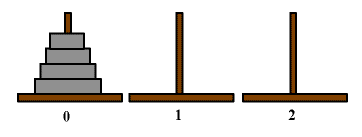
The task is to move the disks from the left (tower 0) to the center (tower 1). Only one disk may be moved at a time, and a larger disk may never be placed on top of a smaller one.
The recursive solution consists of first moving 3 disks from 0 to 2, and then the bottom one to 1. Then, another 3 disks from 2 to 1. Therefore, if you know how to move 3 disks, you can move 4 disks. This can be implemented in the following program.
public class Test
{
public static void main (String args[])
{
hanoi(4,1,2,3); // move 4 disks from 0 to 1
}
static void hanoi (int n, int from, int to, int using)
// Moves n disks from from to to, where using is free.
{
if (n==1)
{
System.out.println("Move disk from "+from+" to "+to);
}
else
{
hanoi(n-1,from,using,to);
System.out.println("Move disk from "+from+" to "+to);
hanoi(n-1,using,to,from);
}
}
}
The program output is a sequence of instructions specifying where to move the next disk.
Move disk from 1 to 3 Move disk from 1 to 2 Move disk from 3 to 2 Move disk from 1 to 3 Move disk from 2 to 1 Move disk from 2 to 3 Move disk from 1 to 3 Move disk from 1 to 2 Move disk from 3 to 2 Move disk from 3 to 1 Move disk from 2 to 1 Move disk from 3 to 2 Move disk from 1 to 3 Move disk from 1 to 2 Move disk from 3 to 2
The program looks easy, but is probably difficult to understand at first.
As an example of a fast sorting algorithm, we present the Quicksort method. The logic of the program is somewhat difficult to understand.
The algorithm used is as follows:
This is, of course, a recursive procedure.
public class Test
{
static public void main(String args[])
{
int n = 100;
double v[] = new double[n];
int i;
for (i = 0; i < n; i++)
v[i] = Math.random(); // n random numbers
QuickSort(v, 0, n - 1); // sort
for (i = 0; i < n; i++)
System.out.println(v[i]);
// and output.
}
static void QuickSort(double a[], int loEnd, int hiEnd)
// Sort the section between a[loEnd] and a[hiEnd]
{
int lo = loEnd;
int hi = hiEnd;
double mid;
if (hiEnd > loEnd) // otherwise nothing needs to be done!
{
mid = a[(loEnd + hiEnd) / 2];
// Take a medium-sized element (hopefully)
// Separate into smaller and larger ones:
while (lo <= hi)
{
while ((lo < hiEnd) && (a[lo] < mid))
lo++;
// from left to right,
// as long as there's nothing to do
while ((hi > loEnd) && (a[hi] > mid))
hi--;
// from right to left
// as long as there's nothing to do
if (lo <= hi) // two elements are incorrect!
{
swap(a, lo, hi); // swap
lo++; // now they are positioned correctly
hi--;
}
}
// Sort right:
if (loEnd < hi)
QuickSort(a, loEnd, hi);
// Sort everything smaller mid
if (lo < hiEnd)
QuickSort(a, lo, hiEnd);
// Sort everything larger mid
}
}
static void swap(double a[], int i, int j)
// Swap a[i] with a[j]
{
double h;
h = a[i];
a[i] = a[j];
a[j] = h;
}
}
How can you find data in a sorted array? This can be done quite quickly using an interval division method. If you are looking for a number in the array range i to j, you can compare the number with the element in the middle (i+j)/2 and thereby split the range into two parts.
static int binSearch (double v[], double x)
// search the sorted double array for x
{
return binSearch(v,x,0,v.length);
}
static int binSearch (double v[], double x, int i, int j)
// search the sorted double array for x between i and j-1
{
int k=(i+j)/2;
if (v[k]==x) return k;
else if (k==i) return -1;
else if (v[k]>x) return binSearch(v,x,i,k);
else return binSearch(v,x,k,j);
}
The algorithm is most easily programmed recursively. To do this, you pass the double array to be searched, the value to be found, and the interval limits i and j for the indices. Then, a middle index k=(i+j)/2 is calculated, and it is tested whether this index equals the value being searched for. Otherwise, the search continues to the right or left.
Note that the algorithm must terminate. This occurs when j equals i+1 . In this case, k equals i , and we pass -1 , which means "not found". The order in which the tests are performed is important.
This example is probably only understandable to mathematicians, as matrix multiplication requires knowledge of this topic. Let A be a square matrix. We calculate A^n for large n . The algorithm used assumes
A n =(A n/2 ) 2
if n is even, or
A n =A*(A (n-1)/2 ) 2
if n is odd. This works recursively, of course, and is a very efficient method.
The program uses as an example a special matrix whose powers are related to the Fibonacci numbers.
Here you can also see how two-dimensional arrays are used as parameters and return values. The size of the arrays is not passed along, but rather read using `length` . Note that the number of columns in a square matrix is the size of `a[0]` (which is the first row of `a` ).
This time we're using JavaDoc comments, as they should be.
/** * Demonstration of the powers of matrices using recursion * * @author reneg */ public class Test { static public void main(String args[]) { double A[][] = { { 0, 1 }, { 1, 1 } }; double B[][] = pot(A, 100); print(B); // print A^n System.out.println(B[0][0] + B[0][1]); // prints 5.731478440138171E20 System.out.println(fibonacci(100)); // prints the same } /** * Calculate A^n using the method of successive squaring * * @param A Quadratic Matrix * @param n potency * @return A^n */ static double[][] pot(double a[][], int n) { if (n == 1) return a; if (n % 2 == 0) return sqr(pot(a, n / 2)); else return mult(sqr(pot(a, n / 2)), a); } /** Calculate the product of two matrices * * @param A * @param B * @return A*B */ static double[][] mult(double a[][], double b[][]) { double c[][] = new double[a.length][b[0].length]; int i, j, k; for (i = 0; i < a.length; i++) for (j = 0; j < b[0].length; j++) { c[i][j] = 0; for (k = 0; k < b.length; k++) c[i][j] += a[i][k] * b[k][j]; } return c; } /** * Calculate A*A * * @param A * @return A^2 */ static double[][] sqr(double a[][]) { return mult(a, a); } /** * Print a matrix. * * @param a */ static void print(double a[][]) { int i, j; for (i = 0; i < a.length; i++) { for (j = 0; j < a[i].length; j++) System.out.print(a[i][j] + " "); System.out.println(""); } } /** * Calculate the nth Fibonacci number * * @param n * @return F_n */ static double fibonacci(int n) { int i; double a = 0, b = 1, old; for (i = 0; i < n; i++) { old = b; b = a + b; a = old; } return b; } }
One of the most fascinating examples of recursive programming is the Merge Sort algorithm . In fact, it can also be used for manual sorting. It is the fastest known general sorting algorithm.
The recursive description is quite simple. We divide the stack to be sorted into two halves, sort each half, and then merge the two sorted halves. This merge is easy because we only need to draw the smaller card from each of the two stacks until one stack is empty. The recursion arises naturally because we sort both halves using the same algorithm.
class MergeSorter
{
// needed as working space
String[] work;
public void sort (String[] array)
{
if (array.length < 2)
return;
// create workspace
work = new String[array.length];
// call recursive sort
sort(array, 0, array.length - 1);
}
void sort (String[] array, int start, int end)
{
// System.out.println(start + "-" + end);
// half point, can be equal to start or end.
int half = (start + end) / 2;
if (half - start > 0) // need to sort first half
sort(array, start, half);
if (end - (half + 1) > 0) // need to sort second half
sort(array, half + 1, end);
// merge sorted parts
merge(array, start, half, half + 1, end);
}
void merge (String[] array, int start1, int end1, int start2, int end2)
{
// aim index to copy into work
int aim = start1;
// remember start index, because we are changing start1
int start = start1;
// Loop breaks if one merge part is exceeded
while (true)
{
if (array[start1].compareTo(array[start2]) < 0)
{
work[aim++] = array[start1++];
if (start1 > end1) // first part is exceeded
{
while (start2 <= end2)
work[aim++] = array[start2++];
break;
}
}
else
{
work[aim++] = array[start2++];
if (start2 > end2) // second part is exceeded
{
while (start1 <= end1)
work[aim++] = array[start1++];
break;
}
}
}
System.arraycopy(work, start, array, start, aim - start);
}
}
public class Test
{
public static void main (String args[]) throws Exception
{
// Create 10 million strings
int N = 10000000;
String[] array = new String[N];
for (int i = 0; i < N; i++)
array[i] = "String " + Math.random();
// create sorter
MergeSorter sorter = new MergeSorter();
// sort with time measurement
long time = System.currentTimeMillis();
sorter.sort(array);
// Arrays.sort(array); // compare to system sort
System.out.println((System.currentTimeMillis() - time) + " msec");
// Check sort
for (int i = 0; i < N - 1; i++)
if (array[i].compareTo(array[i + 1]) > 0)
throw new Exception("Error in Sort");
}
}
The call in the main program, enclosed within the timing, is redirected to a recursive function in the MergeSorter . The `merge` function is quite easy to implement if you use the loop approach shown here with a continuous loop. The strings are stored in the working array `work` and copied from there back to the original array using `System.arraycopy` . This is somewhat faster than copying with a `for` loop.
The algorithm takes about 10 seconds to process 10 million strings. For normal array lengths, it is very, very fast. The internal algorithm performs similarly.
The MergeSorter works this way with the specific data type String and would need to be rewritten for other data types. However, we will later learn about generic data types and interfaces that allow for a more flexible implementation.